Goal: Hone the concept of line integral
Source: 283-CTQsas35
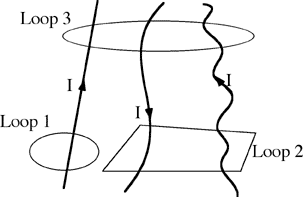
Three wires, each carrying the same current, I, are in a region of
space, as shown below. What could be the result of computing the left
hand side of Ampere’s law, 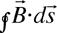 , for the
, for the
three Amperian Loops shown?
- Loop 1: μ0I, Loop 2: 2μ0I, Loop 3: 3μ0I
- Loop 1: -μ0I, Loop 2: 0, Loop 3: μ0I
- Loop 1: μ0I, Loop 2: 2μ0I, Loop 3: μ0I
- Cannot be determined



Commentary:
Answer
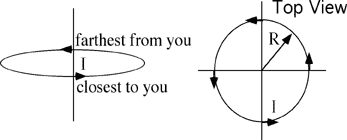
(4) The direction to integrate around the loop is not specified. The
only choice of responses that is possibly true is #2 and this would
require a clockwise integral around loop 1.