Goal: Reasoning regarding electric fields due to distributed charges
Source: 283-395 Electric field from a rod, on its axis.
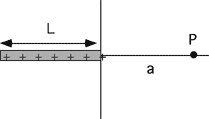
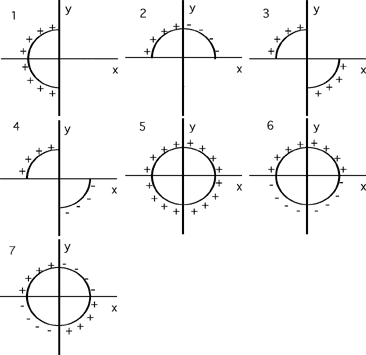
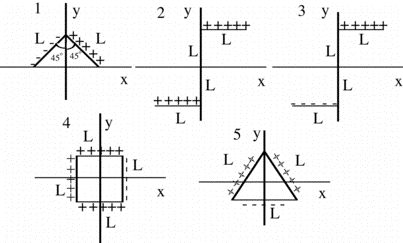
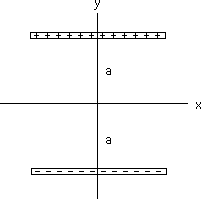
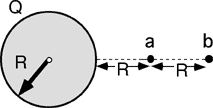
A rod of length L and charge +q
(uniformly distributed) is positioned along the x-axis, as shown to the
right. What is E at point P, a distance a from the origin?
1.
 |
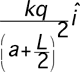2.
 |
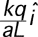3.
 |
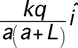4.
 |
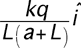5.
 |
Goal: Reason with electric fields
Source: 283-370 E due to circular rods
All of the curved charged rods shown in the image below have the same
radius and linear charge density (though some are positively charged and
others are negatively charged). For which configuration would the
magnitude of E at the origin be greatest?
(6) This problem constitutes a good exercise for students learning the
vector nature of the electric field. There are many good followup
questions, such as; Which configurations have zero field at the origin?,
Order the configurations by increasing magnitude of electric field at
the origin. Stress the value of symmetry for reasoning to the answer. A
negative distribution in a quadrant is equivalent to a positive
distribution in the opposite quadrant, which means that distributions #5
and #7 are equivalent (for purposes of finding the E field at the
origin).
Goal: Reason regarding induced charges and fields
Source: 283-235 Induced charge in conductors
A positive charge per unit area σ is placed on a cylindrical
conductor of inner radius, r = a, and outer radius, r = b. A positive
charge per unit length, λ, is placed along the axis of the
cylinder. What is the charge density (charge per area) on the outer
surface?
(7) The biggest problem for students is finding the induced surface
charge density due to the line charge density.
Goal: Reason regarding electric fields
Source: 283-11, E at origin due to charged rods
For which of the configuration(s) below does the total electric field
vector at the origin have non-zero components in both the x and y
directions?
(6) Only situation 3 meets the condition. A good exercise is to have
students draw the contribution to the field at the origin due to each
rod. The contributions should have the correct relative size and
direction.
Goal: Reason regarding electric fields
Source: 283-10, E at origin due to charged rods
All of the configurations shown below consist of charged rods of the
same length L. The magnitude of the total charge is also the same for
each rod. The total charge in each rod is distributed uniformly.
For which
configuration(s) is the electric field vector at the origin in the
positive x direction?
(4) Because they are given lots of examples involving point charges,
spheres and rings, students often miss the fact that there are many
situations for which the direction of the field can be deduced even
though determining the value or formal expression for the field is way
beyond them.
Goal: Hone the concept of electric field
Source: UMPERG-283-365
Two
uniformly charged rods are positioned horizontally as shown. The top
rod is positively charged and the bottom rod is negatively charged. The
total electric field at the origin
(6) By symmetry the field must point along the y-axis. Students
who do not understand that the field points away from positive charges
and towards negative charges would select #1 thinking that the fields
cancel.
Goal: Reasoning about electric fields
Source: 283 ring, E on axis
A ring
of radius R with charge +Q (uniformly distributed) is positioned as
shown. What is the electric field at a point on the axis, a distance x
from the origin?
None of the above.
(4) Discuss how the form of the field can be reasoned from symmetry and units. Together with limiting value as x goes to zero, this uniquely singles out one answer.
A good follow-up activity is to have students sketch a graph of the field and potential along the x-axis.
Goal: Hone the concept of electrostatic potential
Source: 283-420 Change of PE
A uniform volume distribution of
charge has radius R and total charge Q. A point charge -q is released
from rest at point b, which is a distance 3R from the center of the
distribution. When the point charge reaches a, which of the following is
true regarding the potential energy, U?
(7) Many students use an inverse square dependence appropriate
for fields. Others will take the field at b and multiply by the
displacement. Still others will assert that the potential doubles
because they are using the distance to the surface of the sphere.
Goal: Hone vector nature of electric fields
Source: UMPERG-em97Q
Two uniformly charged rods are positioned horizontally as shown. The
top rod is positively charged and the bottom rod is negatively charged.
The total electric field at the origin
(6) Along the y-axis, by symmetry, the electric field due to either rod
points along the y-axis. At the origin the contribution to each rod is
the same and points down.
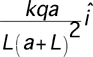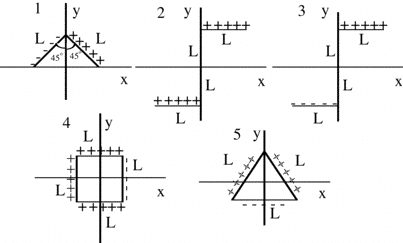
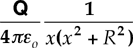
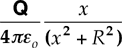
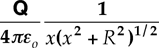
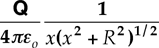
Commentary:
Answer
(3) It is worthwhile having students examine their choice for the
limiting case a->0. Students are inclined to immediately start a formal
calculation rather than think about the problem long enough to figure
out what they really need to know. In this case all but two of the
answers can be ruled out because they do not limit appropriately as the
point P moves toward the origin. If a>>L the field should drop off as
from a point charge. The only answer meeting both these requirements is
3.