Goal: Reason regarding inductors
Source: 283-755 RL equivalent circuit at t small
Consider the following circuit.
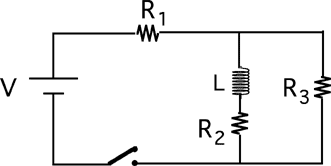
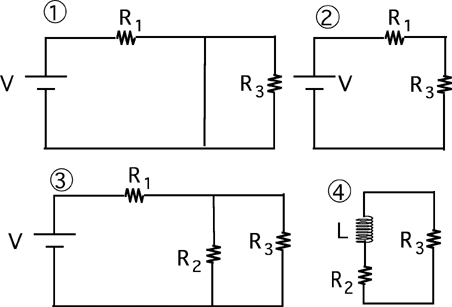
The switch is closed at t=0. Which circuit is equivalent to this circuit
for the instant immediately after the switch is closed?
Goal: Reason regarding inductors
Source: 283-755 RL equivalent circuit at t small
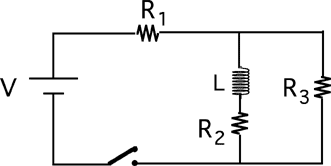
Consider the following circuit.

The switch is closed at t=0. Which circuit is equivalent to this circuit
for the instant immediately after the switch is closed?

Goal: Reasoning regarding inductors
Source: 283-750 LR equivalent at time = infinity
Consider the following circuit.
The switch is closed at t=0. Which circuit is equivalent to this circuit
as t approaches infinity?
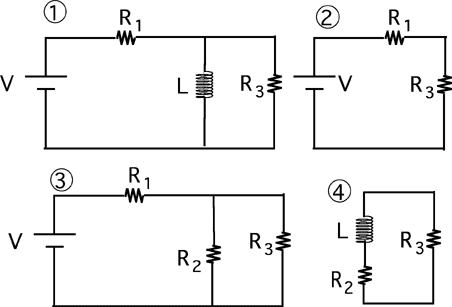
(3) Some students misunderstand the statement that inductors behave as a
short circuit after a long time and select #1 or #2.
This item is best used in conjunction with the previous one. Both should
be asked before discussion of either to reveal whether students just
have the behaviors reversed or evidence a more serious problem.
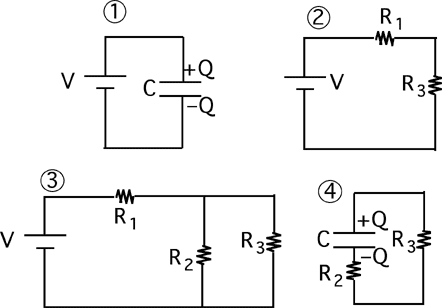
Goal: Reason regarding capacitors
Source: 283-585 RC equivalent circuit at early time
Consider the following circuit.

The capacitor is uncharged when the switch is closed at t=0. Which
circuit is equivalent to this circuit for the instant immediately after
the switch is closed?
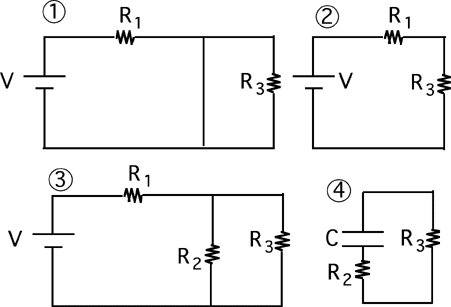
(3) Some students misunderstand the statement that capacitors behave
initially as a short circuit and select #1 or #2.
This item is best used in conjunction with the next one. Both should be
asked before discussion of either to reveal whether students just have
the behaviors reversed or evidence a more serious problem.
Goal: Reason regarding capacitors
Source: 283-590 RC equivalent at t infinity
Consider the following circuit.
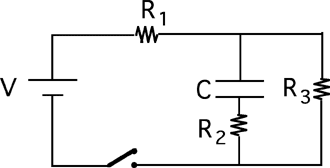
The capacitor is uncharged when the switch is closed at t=0. Which
circuit is equivalent to this circuit as t approaches infinity?
(2) Students often misunderstand the statement that capacitors behave
like an open circuit after a long time.
This item is best used in conjunction with the previous one. Both should
be asked before discussion of either to reveal whether students just
have the behaviors reversed or evidence a more serious problem.
Goal: Reason regarding RC circuits.
Source: 283 – energy dissipated in RC circuit
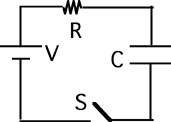
Consider the following circuit. The capacitor is uncharged when
switch S is closed at t = 0. During the charging process the total
energy dissipated in the resistor is:
(2) Students should recognize that if the capacitor ultimately is
charged to Q, the total work done by the battery is QV. Half of this is
stored in the capacitor and half is dissipated in the resistor.
Goal: Reason regarding RL circuits.
Source: 283 – energy dissipated in inductor
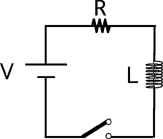
Consider the following circuit. The switch S is closed at t = 0.
The total energy dissipated in the resistor before the current reaches
its maximum value is:
(5) The total work done by the battery is QV where Q is a function of
time which is not limited. The total energy stored in the inductor is
finite. The difference must be the energy dissipated in the resistor.
Since it takes an infinite amount of time for the current to reach its
maximum value, the total amount of energy dissipated is also maximum.
A good follow up question is: Is there a time when the dissipated energy
is equal to the stored energy? If so, what is that time?
Goal: Link energy with electrical quantities
Source: 283 – energy in capacitor
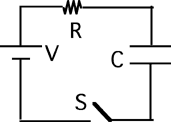
Consider the following circuit. The capacitor is uncharged when switch S
is closed at t = 0. After current stops flowing and the capacitor is
fully charged the energy stored in the capacitor is:
(3) The intent of this question is to provide students the opportunity
to distinguish a correct but uncommon form for the stored energy from a
number of other familiar forms.
Goal: Link energy with electrical quantities
Source: 283-energy in L
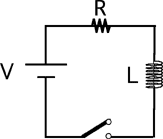
Consider the following circuit. The switch S is closed at t = 0.
After a long time the energy stored in the inductor is:
L^2^/R
RL^2^/2
LV/2R
V/RL
none of the above
(5) This is a good time to discuss with students the general form of
energy expressions as 1/2 something times (something else)^2^.
Goal: Reason regarding circuits
Source: 283 compare dissipated energy
Consider the following circuits. Two identical batteries are connected
to two identical capacitors in series with different resistors. The
capacitors are initially uncharged. Which statement is true regarding
the energy supplied by the batteries to charge the capacitor?
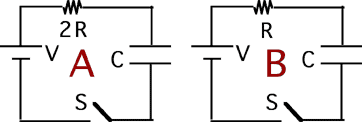
(3) The energy dissipated in the resistor is independent of the
resistance. Consider a time when the capacitor contains some charge Q.
If an additional charge dq is added, the battery does work dqV and the
increment of stored energy in the capacitor is (Q/C)dq. By conservation
of energy, the difference must have been dissipated in the resistor. The
difference, [V-(Q/C)]dq is independent of resistance.
Goal: Reason regarding circuits
Source: 283 Compare dissipated power with inductors
Consider the following circuits. Two identical batteries are
connected to two identical inductors in series with different resistors.
The switch is closed at t=0. Which is true regarding the energy
supplied by the battery to establish current I?
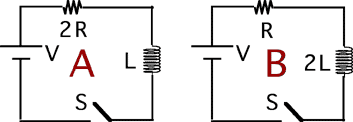
(4) It is not determined that either circuit can achieve the current I.
If I is to be interpreted as the ‘final’ current, then the answer is #2.
The lower the resistance the higher the final current. There is more
energy stored in the inductor if the final current is higher. In
addition, the energy dissipated in the resistor goes as i2R which is
larger for circuit B for every current larger than V/(2R).
Commentary:
Answer
(2) Some students misunderstand the statement that inductors behave
initially as an open circuit and select #1 or #3.
This item is best used in conjunction with the next one. Both should be
asked before discussion of either to reveal whether students just have
the behaviors reversed or evidence a more serious problem.