Goal: Reason with the concept of moment of inertia
Source: UMPERG-ctqpe116
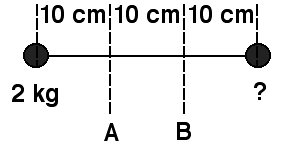
The rotational inertia of the dumbbell (see figure) about axis A is
twice the rotational inertia about axis B. The unknown mass is
Goal: Hone rotational dynamics
Source: UMPERG-ctqpe1246
A system consisting of two masses on a string is rotating with angular
velocity ω on a frictionless horizontal surface. The center of
rotation is the left-hand side of the string (nailed to the table).
The ratio of the tension in the inner string to that in the outer string
is
(3) Many students think the ratio is determined just by the string
lengths and give as an answer either (2) or (4). They fail to draw a
free body diagram for the inner mass and, consequently, fail to realize
that it is the net force on the inner mass that must maintain the
circular motion of the inner mass.
Goal: Hone angular kinematic quantities and distinguish them from linear kinematic quantities.
Source: UMPERG
A mass moves in a circle with uniformly increasing angle.
As the angle θ increases, the linear acceleration of the mass has
…
(2) Students have a lot of difficulty reconciling linear kinematics with
angular kinematics. Unless shown how to take derivatives in polar
coordinates, or shown how to represent rotational kinematic quantities
as vectors, students can only memorize specific relationships.
Some students may answer (1) thinking that ‘towards the center’ is a
direction.
Goal: Problem solving.
Source: UMPERG-ctqpe146
A
child having mass 32kg is standing at the rim of a rotating disk of
radius 1.5m. The disk is free to rotate without friction. The disk has
moment of inertia I = 125kg-m2 and is initially at rest. The
child throws a rock of mass 4kg in the forward tangential direction as
shown in the figure with a speed of 5m/s. The final angular speed of
the disk is most nearly
(7) is the most appropriate response. Initially there is no angular
momentum in the system. The child and disk must rotate clockwise to
balance the angular momentum of the rock. Some students may forget to
add the moment of inertia of child to that of the disk.
Throwing the rock tangentially gives the rock angular momentum relative
to the fixed center of the disk. The disk-child system must have an
angular momentum which is the negative of that of the rock. Thus, it is
possible to find the angular velocity. The angular velocity is
negative, i,e, into the page.
Does the total system have angular momentum just before the rock is
thrown? just after it is thrown?
Does the rock have angular momentum just before it is thrown? just
after it is thrown?
What happens to the child upon throwing the rock? Does the child move?
How?
Have students relate their answer to this question to items 67 and 68.
Goal: Hone the concept of angular velocity and link to rotational inertia and angular momentum
Source: UMPERG-ctqpe122
A child is standing at the rim of a
rotating disk holding a rock. The disk rotates without friction. The
rock is dropped at the instant shown. As a result of dropping the rock,
what happens to the angular velocity of the child and disk?
Answer
(2) is the correct response if the rock is simply dropped. However, some
students selecting this choice may think that the angular velocity is
maintained by some external agency. Students selecting answer (1) are
likely misapplying conservation of angular momentum.
Background
This question is useful for revealing whether students understand the
concept of moment of inertia and its relationship to angular momentum.
Many students reason that after the rock is dropped, the moment of
inertia is smaller and the angular velocity must increase to conserve
angular momentum.
RevealingQ
When dropped, does the rock have angular velocity? Just before being
dropped does the rock have angular momentum? Just after being dropped
does the rock have angular momentum?
Suggestions
It is possible to do a traditional demonstration of the role of moment
of inertia in angular momentum and then just drop the weights when arms
are extended.
Commentary:
Answer
(4) Students can get bogged down in calculations when it is unnecessary
to do detailed calculations. Proportional distances to the axes is all
that is needed. This problem presents a good opportunity to discuss
problem solving procedures.