Goal: Reasoning with energy
Source: UMPERG-ctqpe64
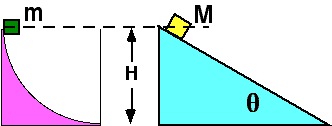
Two
masses, M > m, travel down the surfaces shown. Both surfaces are
frictionless. Which mass has the largest speed at the bottom?
- m
- M
- Both have the same speed
- Cannot be determined
Goal: Reasoning with energy
Source: UMPERG-ctqpe64

Two
masses, M > m, travel down the surfaces shown. Both surfaces are
frictionless. Which mass has the largest speed at the bottom?
Goal: Reasoning with kinematics
Source: UMPERG-ctqpe63

Two
masses, M > m, travel down the surfaces shown. Both surfaces are
frictionless. Which mass has the largest average speed during
their motion?
(1) This problem is intended to promote discussion of average
speed. Both masses have the same speed at the bottom. Mass m has a
larger acceleration in the beginning because the circular track is
vertical at the outset. Although the angle of the incline is not
specified, the angle is irrelevant. All inclines will have the same
average speed. A simple graph of the speed of each mass versus time
shows that m will have the larger average speed.
Goal: Reasoning with energy
Source: UMPERG-ctqpe62
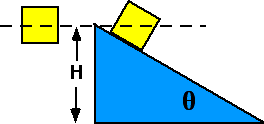
Two
identical blocks fall a distance H. One falls directly down, the other
slides down a frictionless incline. Which has the largest speed at the
bottom?
(3) The only force doing work is gravity and both block undergo
the same vertical displacement.
Goal: Distinguish average velocity from velocity.
Source: UMPERG
A car is initially located at the 109 mile marker on a long straight
highway. Two and one half minutes later the car is located at the 111
mile marker.
What is the velocity of the car?
The correct answer is (7) because only the average velocity can be
determined. However, students who respond (4) should not be
disconfirmed but prodded to be more discriminating when interpreting
questions. They have assumed that the car is traveling with a uniform
speed.
Students should be able to extract kinematical quantities from everyday
situations. They should also have a sense of the size of these
quantities.
What is the speed of the car when it is at the 109 mile marker? How do
you know?
Is it possible for the car to be at rest initially and reach the 111
mile marker two and one half minutes later? If it had constant
acceleration, what would its speed be when it reached the 111 mile
marker?
Have students make a sketch of position vs. time. They probably assume
that the speed is uniform throughout the time interval. Have them
consider other paths that still connect the two known points on the
position vs. time plot. Draw some reasonable path and have the students
describe what the car is doing during that interval.
Goal: Hone the concepts of speed and velocity.
Source: UMPERG
The radius of the Earth is 6,400 km. The speed and direction would you
have to travel along the equator to make the sun appear fixed in the sky
is most nearly
(8) You would attempt to remain underneath the sun as it traveled from
East to West. Some students may be confused by the tilt of the Earth’s
axis and think that the Sun could not remain fixed in the sky if you
were constrained to move along the equator. These students would likely
answer (9).
Students should be able to determine the speed and direction even if
they do not yet have a solid grasp of velocity as a vector.
What is the circumference of the Earth? Does everyone on the Earth
travel at the same speed?
Build a simple model. Most students can readily grasp the result when
the Earth’s axis is perpendicular to the plane of the Earth’s orbit. A
model helps them understand that the tilt of the axis doesn’t matter.
Goal: Hone the vector nature of velocity.
Source: UMPERG-ctqpe142

A
child is standing at the rim of a rotating disk holding a rock. The
disk rotates without friction. The rock is thrown in the RADIAL
direction at the instant shown, which of the indicated paths most nearly
represents the path of the rock as seen from above the disk?
(4) is the correct path if the rock is thrown radially.
Once thrown the components of the velocity of the rock lying in a
horizontal plane are constant so the rock will have a path which is a
straight line.
Identify a coordinate frame. What are the components of the velocity
vector immediately after the rock is thrown?
What is the radial component of the velocity if the rock follows path
(2)?
Is it possible to throw the rock in such a way that the rock follows
path (5)?
This item should be compared to 63.
Goal: Understanding the first law.
Source: UMPERG-ctqpe120
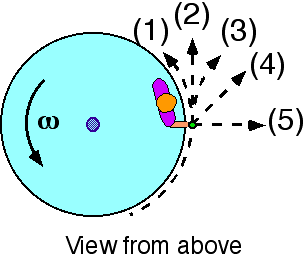
A
child is standing at the rim of a rotating disk holding a rock. The
disk rotates without friction. If the rock is dropped at the instant
shown, which of the indicated paths most nearly represents the path of
the rock as seen from above the disk?
(2) is the correct path if the rock is simply dropped. Some students
selecting answer (3) may be viewing the rock from the child’s
perspective. Some students indicating choice (5) may interpret this
path as ‘straight down’.
This question is similar to others which seek to reveal student
perceptions about path persistence. It is a slightly different context
from the purely horizontal case of a ball rolling on a horizontal
surface around an semicircular section of hoop.
What path would the child see?
What is the velocity of the rock just before it is dropped? just after?
What would the path of the rock have been if the child continued to hold
it?
There are a variety of demonstrations that can be done as followup to
this question. It is important that students perceive the similarity
between the demonstration context and the problem situation.
Goal: linking acceleration and velocity graphically.
Source: UMPERG
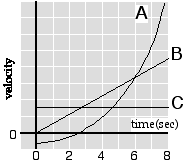
The
plot of velocity versus time is shown at right for three objects. Which
object has the largest acceleration at t = 2.5s?
(6) Objects (A) and (B) have the same acceleration (i.e., they have the
same slope for the velocity vs. time graph at t=2.5s) Object (C) has a
constant velocity (zero slope).
After students have been introduced to acceleration, but before they are
given a procedure for determining the acceleration from a graph of
velocity vs. time. Students should answer this question after they have
gained an understanding of the definition of acceleration, but before
they are given any explicit instruction for how acceleration relates to
a velocity vs. time graph.
How can you determine if an object is accelerating? For which objects
is the velocity changing. What are some examples of objects moving
according to the graphs?
What features about a velocity vs. time graph indicate that an object
has a zero velocity? Zero acceleration? What features indicate a
negative acceleration? Positive acceleration?
Redraw the velocity vs. time graph for object (A) twice more. In one
drawing approximate the curve with three straight line segments. In the
second approximate the curve with 6 straight line segments.
Goal: Associate velocity graph with physical motion.
Source: UMPERG
A soccer ball rolls across the road and down a hill as shown below.

Which of the following sketches of vx vs. t represents the
horizontal velocity of the ball as a function of time?
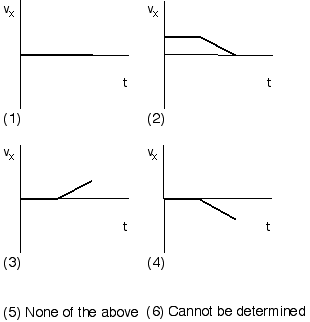

(5) None of the above. The ball crosses the road in a straight line at
a more-or-less constant speed (perhaps slowing down slightly) provided
that the road is in good condition and the rolling friction between the
ball and road is sufficiently small. As the ball rolls down the hill it
will speed up, and so there will be an acceleration in the direction of
motion, with a non zero component to the right. The following graph is
a reasonable representation of the horizontal velocity as a function of
time.
This problem could challenge students in several areas: (1) Can
students recognize how the velocity is changing? What criteria do they
use? (2) Do students realize that as the ball moves down the hill it
speeds up and the x-component of velocity increases? Students may
associate the increase in velocity with the y-direction only. (3) Do
students associate the graph with the terrain over which an object
travels? The process of translation of a motion quantity to a graph can
be very difficult for students. (4) Will students confuse motion
quantities? When students analyze the graphs of velocity vs. time they
may be interpreting the graphs in terms of position instead of velocity.
Is the velocity ever zero? Where does the ball speed up? …slow down?
What is the direction of the velocity while the ball is on the sloped
section? Does the velocity have a non-zero horizontal component?
Set up a demonstration with a horizontal surface and a ramp, both with
the same net horizontal displacement. Roll a ball slowly across the
horizontal surface and down the ramp. Ask students to judge which
horizontal displacement took more time. Over what section (horizontal
surface or ramp) is the velocity larger on average?
Goal: Relating physical motion with graphical representation
Source: UMPERG
Which of the velocity vs. time plots shown below might represent the
velocity of a cart projected up an incline?

Select one of the above or:
(7) None of the above
(8) Cannot be determined
(3) or (4). Initially the cart has a non-zero velocity pointing up the
incline. The speed of the cart decreases as it moves up the incline,
reaching zero at its maximum height. The speed of the cart increases as
the cart moves down the incline. The velocity at the bottom of the
incline points down the incline. Graph (3)/(4) is correct if up/down
the incline is taken as the positive direction.
Students will often associate velocity time graphs with features of the
terrain. Many will pick either (5) because they neglect the vector
nature of velocity and think about the speed.
Is the velocity ever zero? Is the velocity ever positive? … negative?
When? Is the velocity constant? How do you know?
Plotting the position vs. time may help students come up with the
correct plot of velocity vs. time.
Commentary:
Answer
(3) By energy considerations, both would have the same speed.
Students frequently get confused about the mass, thinking that the
larger mass has the greatest potential energy change and therefore has
the greatest speed.