Goal: Unspecified.
Source: Unspecified.
An object’s motion is described by the graph:

What is the instantaneous velocity at t = 3s?
- 0 m/s
- 2 m/s
- 3 m/s
- 4 m/s
- 5 m/s
- Other
Goal: Unspecified.
Source: Unspecified.
An object’s motion is described by the graph:

What is the instantaneous velocity at t = 3s?
Goal: Unspecified.
Source: Unspecified.
An object’s motion is described by the graph:

What is the instantaneous velocity at t = 10s?
None provided.
Goal: Unspecified.
Source: Unspecified.
An object’s motion is described by the graph:

What is the average velocity during the first 10s?
None provided.
Goal: Interrelate representations of kinematical quantities
Source: CT151.2-10
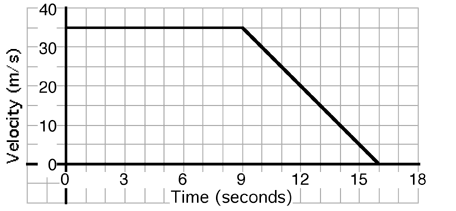
An object’s motion is described by the graph above. The displacement
of the object during the entire 16 seconds is most nearly…
(7) Students have difficulty reading graphs and finding areas.
Goal: Hone the concept of average velocity
Source: CTtil2;12;02
While traveling from Boston to Hartford, Person A drives at a constant
speed of 55 mph for the entire trip. Person B drives at 65 mph for half
the trip and then drives 45 mph for the second half of the trip. When
would B arrive in Hartford relative to A?
(3) Many students are inclined to average the speeds and conclude that
they arrive at the same time. It is often useful to compare this
situation to the one in which time is halved.
Goal: Interrelate representations of kinematical quantities
Source: CT151.2-8
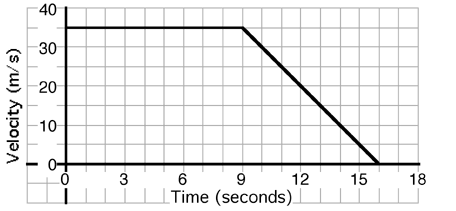
An object’s motion is described by the graph above. The position of the
object at t = 9 seconds is most nearly…
(6) This problem is primarily to determine if students appreciate the
information available from a graph. Many students will determine the
displacement forgetting that the initial position is unknown.
Goal: Link acceleration to the slope of a velocity/time graph
Source: CT151.2-6
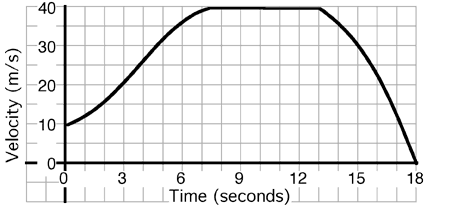
An
object’s motion is described by the graph above. The instantaneous
acceleration at t=10 sec is most nearly…
(1) Useful follow-up questions include; when does the object have
positive acceleration, when negative acceleration; does the object ever
stop?; when is it farthest from the origin?
Goal: Problem solving
Source: UMPERG-ctqpe118
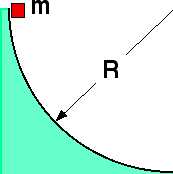
A mass
m slides down a frictionless track of radius R=0.5m. As the mass
reaches the bottom, relative to the center of curvature, its angular
velocity is most nearly:
(1) The velocity near the bottom can be found using energy
conservation.
Goal: Problem solving and developing strategic knowledge
Source: UMPERG-ctqpe103
You are given this problem:
A
block sits on a frictionless incline. Given the angle of incline, the
distance along the incline, and that the block is initially at rest,
find the speed after traveling a distance d.
What principle would you use to solve the problem MOST EFFICIENTLY?
(3) The change in gravitational potential can be found directly.
Alternately, the work done by the gravitational force must be equal to
the change in kinetic energy.
Goal: Problem solving with kinematics
Source: CT151.2-4
Ann is running with a constant speed of 3 m/s on a straight track. Deb
is also running with constant speed but is initially 10 m behind Ann. If
Deb catches up to Ann after Deb has traveled 55 m, how fast is Deb
running?
(6) The correct speed is 3.67 m/s. Students indicating #2 or #3
are likely making an arithmetic error. Have students graph the position
vs. time graphs for each runner.
Commentary:
None provided.