Goal: Recognize a lack of information
Source: CT151.2S02-24
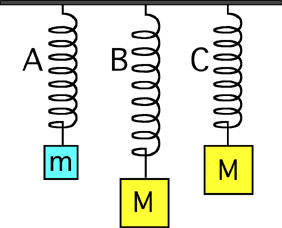
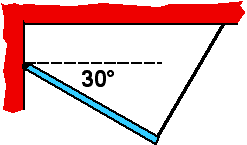
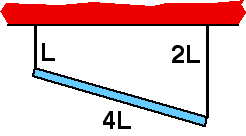
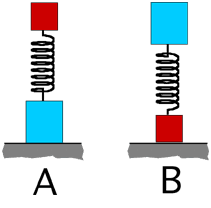
Consider the situations at right. Let m < M. Which spring has
the largest spring constant?
Goal: Hone the concept of average velocity
Source: CTtil2;12;02
While traveling from Boston to Hartford, Person A drives at a constant
speed of 55 mph for the entire trip. Person B drives at 65 mph for half
the trip and then drives 45 mph for the second half of the trip. When
would B arrive in Hartford relative to A?
(3) Many students are inclined to average the speeds and conclude that
they arrive at the same time. It is often useful to compare this
situation to the one in which time is halved.
Goal: Interrelate representations of kinematical quantities
Source: CT151.2-8
An object’s motion is described by the graph above. The position of the
object at t = 9 seconds is most nearly…
(6) This problem is primarily to determine if students appreciate the
information available from a graph. Many students will determine the
displacement forgetting that the initial position is unknown.
Goal: Problem solving with rotational kinematics
Source: CT151.2S02-39
Two masses, attached to the ends of a rigid massless rod, are rotating
about pivot P as shown in the picture below. The mass two meters from P
has speed 0.5m/s. What is the acceleration of the mass one meter from
P?
(2) Every one of the possible wrong responses indicates a common error
that students make. After the problem has been discussed it is useful to
have students find the acceleration of the mass at 2m and see that the
accelerations are in the same ratio as the velocities. Drawing vector
diagrams showing the Δv for each mass is useful for explaining this
relationship.
Goal: Problem solving with dynamics
Source: UMPERG-ctqpe168
A
uniform disk with mass M and radius R rolls without slipping down an
incline 30° to the horizontal. The friction force acting through
the contact point is
(4) This problem requires students to use the 2nd law written in
terms of the CM acceleration and the rotational dynamic relation written
about the CM or the contact point. In either case they also need the
geometric constraint for rolling. This is a difficult problem for
students requiring a lot of additional knowledge, such as the moment of
inertia for a disk and, depending upon solution method, the Parallel
Axis Theorem.
Having gone to the trouble of solving the problem it is best to make
sure that the students glean as much as they can. A good followup
question is which would have a larger friction force, a hoop, a disk or
a sphere. They may try to reason from the acceleration of these objects
that the larger the acceleration, the smaller the friction force. The
friction force depends upon the mass, however, and the question cannot
be answered without knowledge of the masses.
Goal: Problem solving
Source: UMPERG-ctqpe160
A
uniform disk with R=0.2m rolls without slipping on a horizontal surface.
String is pulled in the horizontal direction with force 15N. Moment of
inertia of disk is 0.4 kg-m2. The acceleration of the center
of the disk is most nearly
(2) This problem can be done without knowing anything about the
friction force. To do so, though, requires knowing the Parallel Axis
Theorem for moments of inertia and the constraint between the linear and
rotational rates of motion for a rolling object. An alternate method is
to write the two equations for the linear motion of the center of mass
and the torque relation for rotation about the CM and then eliminate the
friction from the two equations.
Goal: Problem solving with rotational dynamics
Source: UMPERG-ctqpe167
A
uniform disk with mass M and radius R rolls without slipping down an
incline 30° to the horizontal. The acceleration of the center of
the disk is
(5) The acceleration must be smaller than for a mass sliding on a
frictionless incline, but larger than for a hoop. Application of the
rotational dynamic relation τ = Ipαp about point P, the disk’s contact
point with the incline yields an acceleration of g/3. Students must know
the moment of inertia of the disk about its center and use the Parallel
Axis Theorem.
Good discussion questions are: Would a marble have a larger or smaller
acceleration than a coin? Would the angle of the incline matter?
Goal: Problem solve with rotational dynamics
Source: UMPERG-ctqpe156
A
uniform rod is hinged to a wall and held at a 30° angle by a thin
string that is attached to the ceiling and makes a 90° angle to rod.
The tension in the string is 10N. The weight of the rod is about
(4) Some students will use the wrong trigometric function and
conclude that the weight is 40N.
An interesting follow up question is to ask what is the hinge force.
Students often forget that both the sum of the forces and the sum of the
torques must be zero for static equilibrium.
Goal: Reasoning and hone the concept of torque.
Source: UMPERG-ctqpe152
A
uniform rod of length 4L, mass M, is suspended by two thin strings,
lengths L and 2L as shown. What is net torque about the left end of the
rod?
(1) Since the rod does not rotate the total torque must be zero
about any point. Many students overworry this problem not realizing
that, independent of the angle of the rod, the other string is twice as
far as the center of mass of the rod.
Goal: Reason with impulse and energy
Source: CT151.2S02-46
Two
blocks are connected to the ends of a spring as shown. Assume that the
mass is proportional to the size of the block. The spring is compressed
(same amount) and released suddenly. In which orientation will the
system achieve the largest height?
(2) This is a very rich problem for reasoning. It IS possible for
students to reason to the correct solution if they consider appropriate
concepts. To help them along suggest the following: Draw free body
diagrams for each of the masses separately. Combine them to get a valid
free body diagram for the system. Such a process reveals that the normal
force is responsible for the impulse causing the system to jump. The
spring force is internal to the system and does not appear on the
system’s free body diagram.
Students can deduce the answer using analogy or experience. Pogo sticks
or even the human body are analogous systems.
Commentary:
Answer
(8) The objective of this question is to reveal what students are
assuming about the springs. The reasoning behind any incorrect answer
should be thoroughly discussed.